Física- Movimiento Rectilíneo Uniforme (M.R.U.)

Movimiento Rectilíneo Uniforme (M.R.U.)

El movimiento rectilíneo uniforme:
https://youtu.be/ywQRN29OL38

El movimiento rectilíneo uniforme (m.r.u.) es aquel en el que la trayectoria es una linea recta y la velocidad es constante. En este apartado vamos a explicar:

• El concepto de m.r.u.
• Las ecuaciones de este movimiento

 

Definición

A pesar de que encontrar el movimiento rectilíneo uniforme o m.r.u en la naturaleza es bastante extraño, es el movimiento más fácil de estudiar y nos servirá para estudiar otros más complejos. El movimiento rectilíneo uniforme cumple las siguientes propiedades:

• La aceleración es cero (a=0) al no cambiar la velocidad de dirección ni variar su módulo
• Por otro lado, la velocidad inicial, media e instantánea del movimiento tienen el mismo valor en todo momento
  
  Un cuerpo realiza un movimiento rectilíneo uniforme cuando su trayectoria es una línea recta y su velocidad es constante. Esto implica que recorre distancias iguales en tiempos iguales.

  Las ecuaciones del movimiento rectilíneo uniforme son:

  x=x0+v⋅t

  v=v0=cte

  a=0

  Donde:

  • x, x0: La posición del cuerpo en un instante dado (x) y en el instante inicial (x0). Su unidad en el Sistema Internacional (S.I.) es el metro (m)
  • v,v0: La velocidad del cuerpo en un instante dado (v) y en el instante inicial (v0). Su unidad en el Sistema Internacional (S.I.) es el metro por segundo (m/s)
  • a: La aceleración del cuerpo. Su unidad de medida en el Sistema Internacional (S.I.) es el metro por segundo al cuadrado (m/s2)

  Para deducir las ecuaciones del movimiento rectilíneo uniforme m.r.u. hay que tener en cuenta que:

  • La velocidad media coincide con la velocidad instantánea
  • No hay aceleración
    
    
    
    Ejemplo;
    
    
    Imagina que eres un astronauta en la Estación Espacial Internacional. Estás arreglando unos paneles solares averiados, cuando de pronto, al presionar, tu destornillador sale disparado de tus manos. Si no lo atrapas a tiempo, el destornillador estará viajando por el espacio en línea recta y a velocidad constante, a menos que algo se interponga en su camino. Esto sucede porque la herramienta se mueve con movimiento rectilíneo uniforme, o MRU.

    

    Foto de la Estación Espacial Internacional

    Estación Epacial Internacional orbitando nuestro planeta. Créditos: International Space Station orbiting above earth de la National Reconnaissance Office.

    El MRU se define el movimiento en el cual un objeto se desplaza en línea recta, en una sola dirección, recorriendo distancias iguales en el mismo intervalo de tiempo, manteniendo en todo su movimiento una velocidad constante y sin aceleración.

    Recuerda que la velocidad es un vector, entonces, al ser constante, no varía ni su magnitud, ni su dirección de movimiento.

    Condiciones del MRU

    Para que un cuerpo esté en MRU, es necesario que se cumpla la siguiente relación:

    $\Large (v= \dfrac{x-x_0}{t-t_0}) =$left parenthesis, v, equals, start fraction, x, minus, x, start subscript, 0, end subscript, divided by, t, minus, t, start subscript, 0, end subscript, end fraction, right parenthesis, equals Constante

    Donde

    $\Large x$x: es la posición en el espacio y

    $\Large t$t: es el tiempo.

    De esta condición, llegamos a la ecuación del MRU:

    $\Large x = x_0 + v(t-t_0)$x, equals, x, start subscript, 0, end subscript, plus, v, left parenthesis, t, minus, t, start subscript, 0, end subscript, right parenthesis

    Donde:

    $\Large x_0$x, start subscript, 0, end subscript: posición en el instante $\Large t_0$t, start subscript, 0, end subscript

    $\Large x$x: Posición en el instante $\Large t$t

    Esto quiere decir que si conocemos la posición $x_0$x, start subscript, 0, end subscript en el instante $t_0$t, start subscript, 0, end subscript y sabemos cuál es la de la velocidad $v$v, podremos conocer la posición $x$x en cualquier instante $t$t.

    ¡No olvides fijarte bien en las unidades que utilizas y de convertirlas si es necesario!

    Veamos un ejemplo:

    Imagínate que has programado un carro robótico para que tenga una velocidad constante de $10\text{ m/s}$10, start text, space, m, slash, s, end text. ¿Puedes calcular a qué distancia desde el punto de partida estará luego de $30\text{ s}$30, start text, space, s, end text?

    Tienes los siguientes datos:

    $\begin{aligned}v&= 10 \text{ m/s}\\\\ x_0&=0\text{ m}\\\\ t_0&=0\text{ s}\\\\ t&=30\text{ s}\end{aligned}$

    Aplicando la fórmula de MRU:

    $\begin{aligned}x&= 0 \text{ m} + 10 \text{ m/s}(30\text{ s}-0\text{ s})\\\\ x &= 0\text{ m}+ 300 \text{ m}\\\\ x&= 300 \text{ m}\end{aligned}$

    A los $30$30 segundos, tu carro se habrá desplazado $300$300 metros.

    Veamos más ejemplos

    Puedes ver que si el instante y la posición iniciales se asumen como $0$0, la ecuación queda simplificada:

    $\Large x= vt$x, equals, v, t

    Ahora, si sabes que una canica se mueve con MRU, y has medido que en $20$20 segundos, recorre $40$40 metros, ¿podrías hallar su velocidad? ¡Inténtalo

    Veamos otro ejemplo: Si te desplazas con MRU en tu scooter a 10 $\text{ m/s}$start text, space, m, slash, s, end text y quieres llegar al parque que está en línea recta a una distancia de 450 metros, ¿en cuánto tiempo llegarías?

    ¿Puedes resolverlo?

    Compliquemos un poco las cosas.

    Imagínate que un bus de pasajeros va en MRU a $60 \text{ km/h}$60, start text, space, k, m, slash, h, end text. Dos horas más tarde, parte un auto particular desde el mismo punto, con una velocidad de $80 \text{ km/h}$80, start text, space, k, m, slash, h, end text.

    a) ¿Cuántos kilómetros ha recorrido el bus de pasajeros al momento de partida del auto?

    b) ¿A qué distancia del punto de partida se encuentran ambos vehículos?

    Resolvamos esto juntos:

    Primero, escribe los datos:

    $\begin{aligned}v_b&: 60 \text{ km/h}\\\\ v_a&: 80 \text{ km/h}\\\\ t_1&: 2 \text{ h}\end{aligned}$

    Cuando el auto parte, el bus viene recorriendo con MRU:

    $\begin{aligned}x&=vt\\\\ x&= 60 \text{ km/h}\times 2 \text{ h}\\\\ x&= 80 \text{ km}\end{aligned}$

    Cuando el auto parte, a mayor velocidad, el bus lleva recorridos ya $80 \text{ km}$80, start text, space, k, m, end text. La pregunta b) nos indica que ambos deben encontrarse, es decir, deben llegar al mismo punto en el mismo instante.

    

    $80\text{ km}$$x_{\text{b}}$Bus$x_{\text{a}}$Auto

    Representación gráfica del problema enunciado.

    Esto quiere decir que el auto tendrá que recorrer la distancia “$x_a$x, start subscript, a, end subscript” en el mismo tiempo que el bus recorre la distancia “$x_b$x, start subscript, b, end subscript”.

    De esta manera, tenemos:

    $\begin{aligned}x_b&= 60 \text{ km/h}\times t\\\\ x_a&= 80 \text{ km/h}\times t\end{aligned}$

    Eso significa que para ambos, el valor del tiempo es el mismo, la incógnita “$t$t”.

    Además, por la imagen, podemos deducir que:

    $x_a = x_b+ 80 \text{ km}$x, start subscript, a, end subscript, equals, x, start subscript, b, end subscript, plus, 80, start text, space, k, m, end text

    Reemplazando:

    $\begin{aligned}80 \text{ km/h}\times t&= (60 \text{ km/h} \times t) + 80 \text{ km}\\\\ 20 \text{ km/h}\times t&= 80 \text{ km}\\\\ t &= 4 \text{ h} \end{aligned}$

    Luego,

    $\begin{aligned}x_a&= (80 \text{ km/h})(4 \text{ h})\\\\ x_a&= 320 \text{ km}\end{aligned}$

    Entonces,

    a) Cuando el auto particular parte, el bus ya ha recorrido $80 \text{ km}$80, start text, space, k, m, end text.

    b) Ambos vehículos se encuentran cuando están a una distancia de $320 \text{ km}$320, start text, space, k, m, end text del origen.

    ¿Y cuando los móviles se mueven de manera perpendicular?

    Si dos móviles se mueven de manera perpedicular, ¿podemos hallar sus distancias o velocidades aplicando las fórmulas de MRU?

    La respuesta es sí, si es que tienes los datos necesarios. Solo necesitamos recordar el Teorema de Pitágoras

    Por ejemplo:

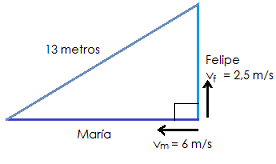
    Dos amigos parten en patinetas desde un mismo punto en direcciones perpendiculares. Felipe va a $2.5 \text{ m/s}$2, point, 5, start text, space, m, slash, s, end text mientras María va $6 \text{ m/s}$6, start text, space, m, slash, s, end text. ¿En cuánto tiempo estarán a $13$13 metros de distancia?

    Nos están pidiendo en qué tiempo $t$t, Felipe y María se encontrarán a una distancia de $13$13 metros.

    María y Felipe parten en direcciones perpendiculares desde el mismo punto. Si graficamos sus recorridos y la distancia que los separa, vemos que se forma un triángulo recto, en el que $13\text{ m}$13, start text, space, m, end text es la hipotenusa y las distancias que recorren Felipe y María, son los catetos. Veámoslo gráficamente:

    

    Gráfica de los movimientos de María y Felipe.

    Ya que ambos se mueven con MRU, podemos reemplazar sus distancias como el producto de sus velocidades por el tiempo $t$t que les toma estar separados $13 \text{ m}$13, start text, space, m, end text. Entonces, los catetos serían:

    $\begin{aligned} \Large d_f &= v_ft\\\\ \Large d_m &= v_mt \end{aligned}$

    Tomando en cuenta el teorema de Pitágoras:

    $(d_f)^2 +(d_m)^2=13^2$left parenthesis, d, start subscript, f, end subscript, right parenthesis, squared, plus, left parenthesis, d, start subscript, m, end subscript, right parenthesis, squared, equals, 13, squared

    Reemplazamos las distancias:

    $(v_ft)^2 + (v_mt)^2 = 13^2$left parenthesis, v, start subscript, f, end subscript, t, right parenthesis, squared, plus, left parenthesis, v, start subscript, m, end subscript, t, right parenthesis, squared, equals, 13, squared

    Utilizamos los datos que tenemos:

    $\begin{aligned}(2.5t)^2 + (6t)^2 &= 169\\\\ 6,25t^2 + 36t^2 &= 169\\\\ 42.25t^2 &= 169\\\\ t^2 &= \dfrac{169}{42.25}\\\\ t^2 &= 4\\\\ t &= 2\text{ s}\end{aligned}$

    Es decir, luego de $2$2 segundos, Felipe y María se encontrarán separados por una distancia de $13$13 metros.

    Gráficas MRU

    Ahora que ya estás familiarizado con las fórmulas del MRU, vamos a mostrarte cómo puedes resolver problemas cuando tienes gráficas de velocidad vs. tiempo.

    Si deseas puedes repasar las gráficas de posición tiempo.

    Cuando haces una gráfica de velocidad vs. tiempo, obtienes una recta paralela al eje $\Large x$x (eje del tiempo), como en el ejemplo siguiente:

    

    $\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{5}$$\small{6}$$\small{7}$$\small{8}$$\small{9}$$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{5}$$\small{6}$$\small{7}$$\small{8}$$\small{9}$$v (m/s)$$t (s)$

    Gráfica de velocidad vs. tiempopara MRU

    Si deseas calcular la distancia recorrida en un $t_1$t, start subscript, 1, end subscript desde $t=0$t, equals, 0, sólo debes calcular el área bajo la gráfica en este punto, ya que:

    $\Large x= vt$x, equals, v, t

    Entonces, tendrías, gráficamente:

    

    $\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{5}$$\small{6}$$\small{7}$$\small{8}$$\small{9}$$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{5}$$\small{6}$$\small{7}$$\small{8}$$\small{9}$$v (m/s)$$t (s)$

    El área bajo la gráfica es la distancia recorrida.

    El área $A1$A, 1 es la distancia recorrida por el objeto hasta el instante $t_1$t, start subscript, 1, end subscript.

    Por ejemplo,

    El desplazamiento de un corredor presenta la siguiente gráfica velocidad vs. tiempo:

    

    $\small{2}$$\small{4}$$\small{6}$$\small{8}$$\small{10}$$\small{12}$$\small{2}$$\small{4}$$\small{6}$$\small{8}$$\small{10}$$\small{12}$$v (m/s)$$t (s)$

    Gráfica de velocidad vs. tiempo de un corredor.

    Calcula:

    a) La distancia que ha recorrido hasta el instante $t = 3 \text{ s}$t, equals, 3, start text, space, s, end text

    b) Si luego de $3$3 segundos de la partida, el corredor pasa por un punto de observación, en donde su entrenador empieza a tomar el tiempo, ¿Cuál es la distancia desde el origen hasta que el cronómetro del entrenador marque $10 \text{ s}$10, start text, space, s, end text?

    c) ¿Cuál sería el desplazamiento recorrido hasta los $8$8 segundos?
    
    
    
    SOLUCION 
    

    Según el gráfico, el corredor va a una velocidad constante de $10 \text{ m/s}$10, start text, space, m, slash, s, end text

    a) La distancia recorrida se define como:

    $\Large x = vt$x, equals, v, t

    A los 3 segundos de iniciada la carrera, la distancia recorrida será:

    $\begin{aligned}x_o&= (10 \text{ m/s})(3 \text{ s})\\\\ x_o&= 30 \text{ m}\end{aligned}$

    b) El corredor llega al punto de observación a los $3$3 segundos, por lo que ha recorrido $30 \text{ m}$30, start text, space, m, end text. El entrenador, desde ese punto, toma el tiempo hasta que su cronómetro marque $10 \text{ s}$10, start text, space, s, end text.

    Desde el punto de observación del entrenador, la distancia recorrida por el corredor, será de:

    $\begin{aligned}x_e&= (10 \text{ m/s})(10 \text{ s})\\\\ x_e&= 100 \text{ m}\end{aligned}$

    Sabemos que para llegar al punto de observación, el corredor ya ha recorrido 30 m, por lo que la distancia desde el punto de partida hasta que el cronómetro de su entrenador marque $10 \text{ s}$10, start text, space, s, end text es:

    $\begin{aligned}d_t&= x_o + x_e\\\\ d_t&= 30 \text{ m} + 100 \text{ m}\\\\ d_t&= 130 \text{ m}\end{aligned}$

    c) ¿Cuál es la distancia recorrida en el instante $8\text{ s}$8, start text, space, s, end text? En el segundo $8$8, tenemos:

    $\begin{aligned}x &= (10 \text{ m/s})(8 \text{ s})\\\\ x&= 80 \text{ m}\end{aligned}$

    Y su representación gráfica sería:

    

    $\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{5}$$\small{6}$$\small{7}$$\small{8}$$\small{9}$$\small{10}$$\small{11}$$\small{1}$$\small{2}$$\small{3}$$\small{4}$$\small{5}$$\small{6}$$\small{7}$$\small{8}$$\small{9}$$\small{10}$$\small{11}$$v (m/s)$$t (s)$

    Representación gráfica de la distancia recorrida.

    ¡Y así  ya estás listo para hacer tus propios cálculos!